Some notes on javascript jit and deopt
Recently I read a fantastic article walking through jit optimizations and how changes to source code could impact those: Side effecting a deopt.
As I shared it with folks, a few of them had some questions about low level optmizations in general and I wrote this as a little explainer for people who are interested in learning more about how javascript runtimes can model/compile/jit/execute their js code. So I wrote this explainer to go along with the original article. Important: please read the original article first or have it pulled up next to this article.
My goal is that by the time we’re done the reader understands a bit more about:
- How their computer can model arbitrary property/value pairs (
Objects) - How their computer can model
Objectswith fixed properties (what many languages would call a struct, or even a class) - Some basics about how a javascript engines can observe how a value runs through the system
Understanding hexadecimal notation and RAM⌗
Many programs that deal with memory addresses use hexadecimal. So instead of saying “20th byte” they say “0x14”. Base 16 just adds 6 extra “digits” and uses
a-f to represent them. So here’s a few numbers in hex and base 10. We often write a prefix 0x for hex numbers to let you know they aren’t base 10.
| base 10 | hex |
|---|---|
| 1 | 1 |
| 10 | a |
| 11 | b |
| 16 | 10 |
| 17 | 11 |
| 20 | 14 |
For those who like a more theoretical description: the idea is that any number we work with like 123 really means: 1*10^2+2*20^1+3*10^0. If you look at our 0x14 example that means:
0x14 = 1*16^1+4*16^0 == 20.
About the only time I mention hex is when discussing the output of optimization tools and it’s really simple
because we’ll deal with things like 0x2 which is 2. And 0xc which is 13.
Disclaimers:⌗
I’m going to be using the madeup phrase “RAM indexes”. The real world calls “RAM indexes” pointers. I’m
hopeful that using “RAM index” as if RAM is an array of bytes is clearer for the target audience. But feel free
to translate statements like RAM[foo] to *foo. Similarly I will talk alot about records that are packed,
the normal industry nomenclature would probably be C struct (with some caveats around packing, padding, field ordering, etc).
I’m pretending in this example that our computers have byte sized words and that ASCII is great because
32bit/64bit and utf8/utf16 don’t add anything to this post and we’d have to count in multiples of 4 or 8.
Finally my hashtables aren’t fast at all. I literally just want people to conceptualize the basic idea of hashing a key to find a bucket
as an alternative to some sort of linear search.
How to represent data in RAM⌗
The atomic unit of data we’ll talk about today is a byte. It’s a series of 8 ones and zeros. Or it’s a number between 0 and 255 (because 2^8=256).
If we want to model some sort of record on the computer, such as a person who has a numeric id and a numeric age, we have to come up with a way of
representing those objects in memory and referring to them. Most of the readers here understand what I mean when I say something like let Person = {id:0, age:24}, but computers don’t.
The simplest way to represent a person “object” then is as 2 bytes next to each other. The first one is their id. The second one is their age. Let’s write out
an array of 2 persons in RAM:
let persons = [{id:1, age:24}, {id:2, age:28}]
| RAM index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| RAM value | 1 | 24 | 2 | 28 | 0 | 0 | 0 | 0 | 0 |
| Field name | id | age | id | age |
So now if you tell a computer where the object starts (via pointer or RAM index), it knows the id is at offset 0, and the age is at offset 1. It knows the size of a person record (2 bytes).
If it needs to operate on those values (LOAD/STORE/MOV low level assembly instructions)
it can directly write machine code that uses those offsets. Let’s write some psuedocode for returning the age of the 2nd person that somewhat mirrors the actual instructions your computer
executes.
let persons_array = ;// some number that is an index into RAM
let size_of_person = 2;
let age_offset = 1;
person_2_age = RAM[
persons_array +// where the array starts
size_of_person +// skip ahead 1
age_offset // age is 2nd value
];
// or equivalantly: one addition. one ram lookup.
person_2_age = RAM[persons_array+3];
Let’s show one more example for strings. Unfortunately strings are variable length. So if you have a record like let person = [{id:"id2", age:29}, {id:"id10", age:40}] those
strings can’t be packed into the same orderly layout as above where each field starts at a fixed offset. We typically store the strings somewhere else and store the RAM index of that location in the person record. Let’s draw that out: because these
strings are variable length we use a special marker character called null or \0 to indicate end of string. This is how the C programming language represents strings historically.
| RAM index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RAM value | 4 | 29 | 8 | 30 | i | d | 2 | \0 | i | d | 1 | 0 | \0 |
| field name | id | age | id | age |
The big thing to notice here is the RAM value for the id. 4 and 8. Those correspond to RAM index 4 and 8. Saying “here’s a fixed sized number who’s value is where you can find the variable
sized data”. So now you have enough background to understand a really basic record/object/struct type. This is an idealized example, in the real world the actual layout can be more complicated but
for our purposes today this is a good enough mental model of “how to layout an object in memory to make it easy for the CPU to get your data”.
Hashtable basics⌗
Now the problem is that the above techniques do not allow us to deal with arbitrary field names. We can’t add fields later on or that would mess up all the calculations like “load the 2nd byte of the
record to get the age”. Javascript Objects allow any number of property/value pairs (in the context of hashtables properties are called keys) and people need to quickly look up a key when they write x.foo. Let’s sketch a couple ways people could store those in memory.
The simplest method is to put all the values right next to each other one after another and use \0 to separate them. Here’s a way to encode {"key1":"value1", "key2":"value2"}
| RAM index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RAM value | k | e | y | 1 | \0 | v | a | l | u | e | 2 | \0 | k | e | y | 2 | \0 | v | a | l | u | e | 2 | \0 |
So if we stored data this way we could pretty easily write some psuedocode for looking up a key/value pair. Just compare the current key in memory with the
property name you are looking for byte by byte. If it doesn’t match, skip the next value until you find a null, and start over. Unfortunately this would be slow because
the farther along your key is, the longer you have to search. So we have something called hashtables. The basic idea of a hashtable is we have some function to convert our
keys to numbers. Then we convert those numbers to a bucket index. A hashtable has several fixed sized buckets right next to each other in RAM. So I might have 10 buckets and when I store “foo” I run a
function which says hash(“foo”) = some random number like 12313213
and then I convert that to a bucket index by saying 12313213%10 = 3. Then in bucket number 3 I store something like: foo\0value\0 (well actually it’s fixed sized. In bucket number 3 I store the RAM index of some other piece of memory that holds foo\0value\0. The great thing about this
is that as long as there are no collisions (2 different keys that go to the same bucket) I can find any property without looking at all the data. The overhead for finding a value in a hashtable
without collisions just depends on how long it takes to run hash(key) and not on the number of keys in the hashtable. I can handle collisions (multiple properties
ending up in the same bucket) by just using the strategy listed above and smashing key value pairs together. Without going into too much detail, real world hashtables have better strategies for minimizing collisions by detecting
when they are close to full and resizing. Sometimes instead of a long chain of key/value pairs they have another hashtable, or a tree. But for today let’s try and show an example of how a 3 key value pairs might be represented in a simple 2 bucket hashtable. The example record is: let person = {name: "bob", id: "id3", age:"21"} I’m going to
draw this as a graph and then also as a linear array of bytes if we just append key/value pairs when there’s a collision.
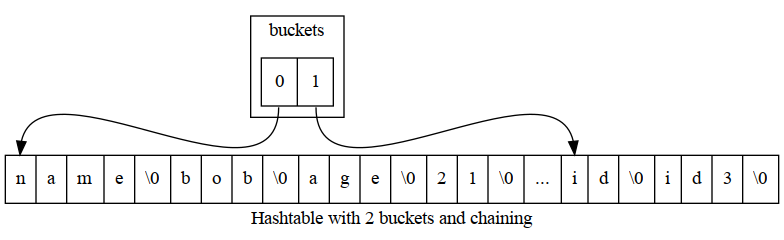
Here’s a table of numbers for representing the same thing. We have a person value which consists of a bucket count and a buckets RAM index. The bucket’s RAM index is where the bucket list starts. Next up we have the 2 buckets. In the real world all of this wouldn’t be packed so close. Which is important for adding more buckets and more key/values. Our first bucket points to index 4, which is where they key/value pair “name:bob” is stored, etc.
| RAM index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RAM value | 2 | 2 | 4 | 20 | n | a | m | e | \0 | b | o | b | \0 | a | g | e | \0 | 2 | 1 | \0 | i | d | \0 | i | d | 3 | \0 |
| field | bucketCount | bucketRamIndex | bucket[0] | bucket[1] |
So this should give you a basic idea that looking up a hashtable key stays fast as you add more items, as long as you don’t have alot more items than buckets. But now instead of the
cpu being able to translate something like person.name into a fixed offset from person, it must instead do the following psuedocode.
// imaginary ram already defined
let RAM = [];
// RAM index where person is located.
let person = 0;
// we've defined it to be the 1st element
let bucketCountOffset = 0;
//we've deinfed it to be the 2nd element
let bucketRamIndexOffset = 1;
// the size of the bucket would have to be stored
let bucketCount = RAM[person+bucketCountOffset]
// hash is defined elsewhere. It takes a string and returns an integer.
let bucketNumber = hash("person")%bucketCount
let startOfbuckets = RAM[person+bucketRamIndexOffset]
let bucketRAMIndex=RAM[startOfBuckets+bucketNumber]
// search_bucket searches a chain of "key\0value\0key\0value\0" pairs.
let age = search_bucket(bucketRAMINDEX, "name");
Note that this requires us to look at several bytes in the property name, do some math, and load several values from RAM just to get to where age is stored. Going into the latency of all these operations is beyond the scope here, but it’s safe to say that two things that often make code slow are:
- Searching for values without any ordering/index
- A bunch of chained RAM lookups such as the 3 RAM lookups we had to do, one of which was chained (often referred to as pointer chasing).
Optimizing a hashtable⌗
So now the optimizations javascript runtimes want to do start to make sense. Any js Object could be a full hashtable, but since so often
js Objects have fixed property names, the runtime would prefer to represent them similar to the 2 byte packed format we used above for person. In fact
it turns out that this happens pretty often. After all our example above where we store a list of objects with the same structure comes up pretty often.
Javascript runtimes detect these patterns and optimize the storage layout and data access. It’s alot harder than you’d expect because javascript is such a dynamic language. So not only must they make the optimizations based on assumptions like “nobody will add keys to this object”, but they must keep track of when those assumptions are violated and fall back to regular hashtables or unoptimized code. They have to do this entire dance on a time/memory budget because afterall they are trying to speed up your code so if their transformations and untransformations aren’t fast enough, they’ve failed at their purpose.
So a good mental model is “javascript runtimes look at data access and speculatively optimize the storage, while maintaining a list of assumptions and dependencies that may invalidate their assumptions. They might have to deoptimize/reoptimize if one of those assumptions changes”.
A simple example to optimize⌗
Let’s look at a javascript function from the blog:
const x = { foo: 1 };
function load() {
return x.foo;
}
console.log(load());
Now just by looking at this function it’s pretty easy to see that in the absence of “funny business”
(certain javascript dynamic features that can cause weird things to happen) it seems like our
entire program could easily be reduced to console.log(1). Let’s trace through how a js engine
might execute each version of the program.
Execution trace⌗
- Create a new string value
"foo" - Create a new number value
1 - Create a new Object and store the above key/value pair in it (which involves hashing and finding a bucket)
- Call the
loadfunction. - Find a variable named
x(note that because it’s not defined in the current function sometimes we might actually does have to “look farther” to noticexis a global variable). - Lookup the value of the
fooproperty onx. This could involve hashing the string"foo"to some number to get a bucket to seach for a value. - Return that value
1 - Call
console.log()with the value1
I’m intentionally trying to omit some boring details while giving you an idea of the work the CPU is doing. What’s important if we’re trying to optimize the performance of load
is to notice that we’re probably doing alot of work hashing the foo key to find where 1 is stored. But we’re smart and we looked at the code and decided that we can replace all the above steps
with just the last one : call console.log() with the value 1. And that is why in the referenced blog post the author points out that the runtime debug information printed out:
0x280008150 130 d2800040 movz x0, #0x2
// The value is 0x2, and not 0x1 because it's been tagged.
Don’t worry about anything but 0x2. That statement is essentially the proof that the optimizer reduced our function call and our object property lookup
down to just the value 1. Javascript uses something called tagged numbers so you’ll have to trust me that in this case 2 on the computer means one in javascript. It’s part
of how javascript distinguishes between a number and an Object at a certain RAM index.
Let’s also look into what assumptions/observations the runtime made in order to make the assumption that
console.log(load()) is console.log(1). This is not an exhaustive list:
- We have to assume that
load()invokes the load function defined above, it can’t have been overridden. - We have to assume that nothing has changed x.foo (the const means x is always the same object, not that the object is immutable)
- We have to assume nobody has messed with the object’s prototype using
x.__defineGetter__("foo", function() { return 2})
And there are some more dependencies that are an artifact of how the runtime implements optimization.
Causing a deopt by changing something that looked constant⌗
So back to reading “side effecting a deopt”: Now we understand why x.foo=5 causes deoptimization/reoptimization.
What’s fascinating is that in their examples v8 didn’t fall back to a completely unoptimized path. Instead
of assuming load always returned 1, is fell back to LoadTaggedField(0xc, decompressed). I’m going
to be a little lazy and not dive deep into the implementation here, and instead assume that means
the code is essentially doing is analogous to what we’ve described as modeling the data for x as record
who’s with one integer field. Let’s write a human readable description of what the runtime has now optimized our function to.
I’ll include an offset called foo_offset just like we did above
for person and age. I’m also
going to invent a new function. Typically in C this is called & for “address of” (or RAM index)
I’ll call it ram_index().
So a psuedocode version of the new optimized code is below: we essentially load the foo property
from a fixed offset of the RAM index where x is stored.
let foo_offset=0
console.log(RAM[ram_index(foo)+foo_offset]);
// For the c folks
// console.log(*(&(foo+foo_offset)))
Expando⌗
We can now pretty easily talk about the effects of taking our optimized value x and adding new properties:
x.__expando = 2;
This causes a deoptimization because the compiler went through all this trouble to figure out that x had just one property that was a number. Now it has 2. So it has to decide whether it wants to create a new optimized storage layout for x with just 2 numbers squished together or whether it should hold off on optimizing. There’s no one right answer, but clearly the previous work was invalidated.
Spooky action at a distance⌗
The last example in the blog post is a fun one. They took our existing optimized code and added a new variable:
const y = {foo:1};
y.__expando = 4;
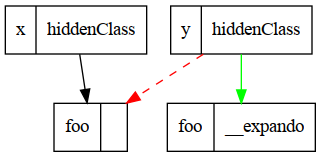
What’s surprising is this code causes x to become deoptimized! There’s no fundamental reason why this has to be true but the short answer is that when the runtime optimizes these variables it essentially has to store a schema (or hidden class) somewhere that says “foo is an integer property at at offset 0”.
When the runtime sees y={foo:1} is does some deduplication so x and y both share the same hidden class/schema. There’s now a dependency here
which is that…. x and y have the same properties.
When we add a new property to y, we break that assumption and x and y can no longer share the same hidden class. There are lots of choices about what the runtime could do, and sorting that out results in another round of deoptimization/reoptimization.
Let’s draw a dependency graph showing the hidden class before/after.
Wrapping up⌗
This is far from an exhausive post, I’m not even sure it was worth writing but so often things like compilers and jits are seen as magic, which to be honest they kind of are, and I’m hopeful that this post helps people unfamiliar with C or jits start to build a mental model of how the computer can map their code and data into something it understands.
There’s no particular action item to take away. No simple way to make your code fast. In fact javascript runtimes contain so many heuristics and tricks that sometimes the code that seems like it should run faster runs slower (for example there are many optimizations around string building and the runtimes can often use fancy datastructures like ropes to speed things up).
If there’s one performance takeaway I would give to the audience of this post, it’s this:
Use a profiler. v8 supports writing symbol maps for linux perf to consume. Chrome has a ton of debug tools. Firefox has great trace viewing infrastructure. Put your application under a magnifying class and try to understand where it’s spending time. Even if your application is faster than it needs to be it’s still nice to know. Is it parsing JSON? Interacting with the DOM? Get a baseline so that as you collect new profiles and develop new features you can spot weird regressions.
And ask yourself if that makes sense. At my current job alot of programs spend alot of time parsing protocol buffers. This is fairly reasonable. At previous jobs our caching edge ingress proxies spent alot of time gzipping uncacheable content and doing TLS. This was somewhat reasonable but pointed to opportunities to improve the customer experience by making more content cacheable.
Hopefully you found some of this informative, now go out there and put an application under a magnifying glass. I guarantee you’ll be surprised at what you find.